The algoritma Kalman Filter bekerja sebagai berikut
Inisialisasi dan .
Pada setiap iterasi
Meramalkan
Perkiraan status prediksi (a priori) Prediksi (a priori) perkiraan kovarians Pembaruan
Sisa inovasi atau pengukuran Inovasi (atau residual) kovarians Optimal Kalman gain Perkiraan keadaan diperbarui (a posteriori) Diperbarui (a posteriori) memperkirakan kovarians
Keuntungan Kalman mewakili kepentingan relatif dari kesalahan sehubungan dengan estimasi sebelumnya .
Saya ingin tahu bagaimana memahami formula untuk mendapatkan secara intuitif ? Pertimbangkan kasus ketika negara bagian dan keluaran menjadi skalar, mengapa keuntungannya lebih besar, kapan
lebih besar
lebih besar
lebih kecil?
Terima kasih dan salam!
sumber















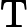

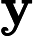
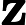



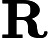
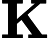

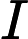

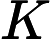
Jawaban:
Saya menemukan cara yang baik untuk berpikir secara intuitif dari Kalman Gain . Jika Anda menulis dengan cara ini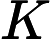
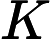
Anda akan menyadari bahwa besaran relatif dari matriks ( ) dan ( ) mengontrol hubungan antara penggunaan filter perkiraan negara yang diprediksi ( ) dan pengukuran ( ).




 ⁻
⁻ỹ
Mengganti batas pertama ke dalam persamaan pembaruan pengukuran
menunjukkan bahwa ketika besarnya kecil, yang berarti bahwa pengukurannya akurat, estimasi keadaan sebagian besar tergantung pada pengukuran.
Ketika keadaan diketahui secara akurat, maka kecil dibandingkan dengan , dan sebagian besar filter mengabaikan pengukuran dengan mengandalkan prediksi yang berasal dari kondisi sebelumnya ( ).
 ⁻
⁻



 ⁻
⁻
sumber
Keuntungan Kalman memberi tahu Anda betapa saya ingin mengubah taksiran saya dengan memberikan pengukuran.
Sebaliknya, jika kecil, maka Anda tahu bahwa keadaan Anda tidak banyak berubah, jadi Anda tidak ingin mengubah perkiraan terlalu banyak setiap saat. Jawaban @ Jav_Rock mengatakan bahwa jika , maka . Dengan kata lain, dia menyiratkan bahwa jika Anda berpikir bahwa keadaan Anda tidak berbeda lagi, Anda tidak mencoba mengubah perkiraan Anda lagi.





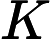


sumber
Jav_Rock mengerti maksudnya. Sebenarnya jika Anda menulis seperti ini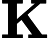
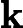
pembilang dari pecahan mewakili ketidakpastian yang disebarkan dari model sementara mewakili ketidakpastian dari pengukuran. Jadi nilai pecahan berarti seberapa besar kita harus mempercayai pengukuran, seperti yang dijelaskan oleh Jav_Rock.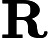
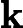
Adapun , itu hanya mengubah pengamatan kembali ke keadaan, karena itu adalah keadaan yang ingin kita perbarui, bukan pengamatan.

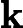
Untuk menyelesaikannya, keuntungan menghitung berapa banyak koreksi yang harus kita ambil dari pengamatan dan mengubah koreksi pengamatan kembali ke koreksi keadaan, yang mengarah pada pembaruan estimasi negara: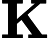
sumber
Saya sedang mengerjakan algoritma Kalman Filter (KF). Saya mengamati bahwa gain kalman berkaitan dengan konvergensi algoritma dengan waktu, yaitu, seberapa cepat algoritma memperbaiki dan meminimalkan residu.
Datang ke persamaan memilih nilai gain kalman awal dan bervariasi dari rendah ke tinggi, yang dapat memberi Anda yang diperkirakan.
sumber