Mengapa Sekolah AS dan Inggris mengajarkan berbagai metode Menghitung Deviasi Standar?

15

Seperti yang saya pahami, Sekolah UK mengajarkan bahwa Standar Deviasi ditemukan menggunakan:

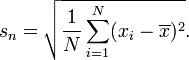
$teks alternatif$

sedangkan Sekolah AS mengajar:

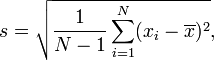
$teks alternatif$

(pada tingkat dasar pula).

Ini telah menyebabkan sejumlah masalah siswa saya di masa lalu ketika mereka mencari di Internet, tetapi menemukan penjelasan yang salah.

Kenapa bedanya?

Dengan dataset sederhana yang mengatakan 10 nilai, tingkat kesalahan apa yang akan terjadi jika metode yang salah diterapkan (misalnya dalam ujian)?

standard-deviation error teaching unbiased-estimator Amos
sumber

4

Saya tidak yakin apakah menandai satu atau yang lain sebagai rumus 'salah' adalah cara untuk memahami masalah ini. Hanya saja yang kedua 'lebih baik' dalam arti bahwa itu adalah penaksir yang tidak bias dari standar deviasi sejati. Jadi, jika Anda peduli dengan perkiraan yang tidak bias maka yang kedua adalah 'lebih baik' / 'benar'.

Saya menganggap rumus sebagai "salah" murni dalam arti bahwa dalam ujian jika Anda menggunakan rumus yang tidak dilarang oleh silabus, Anda akan mendapatkan jawaban "salah". Ditambah lagi jika nilainya bukan sampel populasi per se maka pasti rumus pertama memberikan nilai yang lebih akurat.

Amos

14

Srikant, saya tidak berpikir bahwa yang kedua adalah penaksir yang tidak bias. Kuadratnya adalah penaksir yang tidak bias dari varian yang sebenarnya. Namun, Ketimpangan Jensen menetapkan bahwa ekspektasi fungsi lengkung dari variabel acak tidak sama dengan fungsi ekspektasi variabel acak. Oleh karena itu rumus kedua tidak bisa menjadi penaksir tidak bias dari standar deviasi yang sebenarnya.

Andrew Robinson

Untuk referensi silang: juga ditanya @ m.SE ...

JM bukan ahli statistik

4

Sekolah AS mana pun yang menggunakan teks dasar yang sangat populer oleh Freedman, Pisani, & Purves menggunakan rumus pertama (

), sehingga tampaknya tidak benar untuk mencirikan ini sebagai perbedaan AS vs Inggris.

s_{n}

$s_n$

whuber

18

Formula pertama adalah simpangan baku populasi dan rumus kedua adalah simpangan baku sampel . Rumus kedua juga terkait dengan penaksir yang tidak bias dari varian - lihat wikipedia untuk detail lebih lanjut.

Saya kira (di sini) di Inggris mereka tidak membuat perbedaan antara sampel dan populasi di sekolah menengah. Mereka tentu saja tidak menyentuh konsep seperti penduga yang bias.

csgillespie
sumber

4

Colin, penaksir yang tidak bias dari standar deviasi tidak memiliki representasi bentuk tertutup dalam kasus umum. Apa yang ada adalah penaksir yang tidak bias dari variance (s 2 dalam kasus ini). Patut dicatat bahwa keduanya adalah penaksir yang konsisten dari varians populasi - dan oleh teorema pemetaan berkelanjutan, adalah dua penaksir dari standar deviasi. Poin terkait adalah bahwa n 2 memiliki MSE yang lebih rendah daripada s 2 . Keuntungan tambahan dari memaksakan ketidakberpihakan bisa diperdebatkan.

mornington

@ Tirthankar - sangat ceroboh dari saya. Saya telah mengubah sedikit jawabannya. Terima kasih.

csgillespie

2

Sejauh yang saya ingat, saya diajari perhitungan 'sampel' dalam matematika dan sains GCSE (usia 14-16) dan perbedaan antara populasi dan sampel dan langkah-langkah varians yang terkait dicakup (meskipun tidak secara mendalam) di tingkat A ( umur 16-18). Jadi saya tidak yakin ini perbedaan Inggris / AS yang sederhana.

Freya Harrison

11

Karena belum ada yang menjawab pertanyaan terakhir - yaitu, untuk menghitung perbedaan antara dua formula - mari kita selesaikan itu.

Karena berbagai alasan, pantas untuk membandingkan standar deviasi dalam hal rasio mereka dan bukan perbedaan mereka. Rasionya adalah

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

$|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ $2$

$N$ $5$ $N$ $10$ penilaian atau prediksi semi-kuantitatif (seperti menggunakan 68-95). -99,7 aturan praktis). Perbedaan bahkan lebih penting ketika membandingkanSD, seperti saat membandingkan penyebaran dua set data. (Ketika kumpulan data sama banyaknya, perbedaan secara efektif lenyap sama sekali dan kedua formula mengarah pada kesimpulan yang identik.) Bisa dibilang, ini adalah bentuk penalaran yang kami coba ajarkan kepada siswa pemula, jadi jika siswa menjadi khawatir tentang rumus mana yang akan digunakan, yang dapat diambil sebagai tanda bahwa teks atau kelas gagal untuk menekankan apa yang benar-benar penting.

Kita mungkin ingin memperhatikan kasus sangat kecil $N$ $t$ $z$ $s$ $s_n$

whuber
sumber

6

Ini adalah koreksi Bessel . Versi AS menunjukkan rumus untuk standar deviasi sampel , di mana versi Inggris di atas adalah standar deviasi sampel .

Reed Copsey
sumber

5

Saya tidak yakin ini murni masalah AS vs Inggris. Sisa halaman ini dikutip dari faq yang saya tulis. ( Http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 ).

Cara menghitung SD dengan n-1 di penyebut

Hitung kuadrat dari perbedaan antara setiap nilai dan rata-rata sampel.
Tambahkan nilai-nilai itu.
Bagi jumlah dengan n-1. Hasilnya disebut varians.
Ambil akar kuadrat untuk mendapatkan Deviasi Standar.

Kenapa n-1?

Mengapa membagi dengan n-1 daripada n saat menghitung standar deviasi? Di langkah 1, Anda menghitung perbedaan antara setiap nilai dan rata-rata dari nilai-nilai itu. Anda tidak tahu arti sebenarnya dari populasi; semua yang Anda tahu adalah rata-rata dari sampel Anda. Kecuali untuk kasus-kasus langka di mana mean sampel terjadi untuk menyamai mean populasi, data akan lebih dekat dengan mean sampel daripada ke mean populasi sebenarnya. Jadi nilai yang Anda hitung di langkah 2 mungkin akan sedikit lebih kecil (dan tidak bisa lebih besar) daripada apa yang akan terjadi jika Anda menggunakan populasi sebenarnya yang berarti di langkah 1. Untuk menebusnya, bagi dengan n-1 sebagai gantinya. dari pada Ini disebut koreksi Bessel.

Tapi mengapa n-1? Jika Anda tahu sampel berarti, dan semua kecuali salah satu nilai, Anda bisa menghitung berapa nilai terakhir itu. Ahli statistik mengatakan ada n-1 derajat kebebasan.

Kapan SD harus dihitung dengan penyebut n bukannya n-1?

Buku statistik sering menunjukkan dua persamaan untuk menghitung SD, satu menggunakan n, dan yang lainnya menggunakan n-1, dalam penyebut. Beberapa kalkulator memiliki dua tombol.

Persamaan n-1 digunakan dalam situasi umum di mana Anda menganalisis sampel data dan ingin membuat kesimpulan yang lebih umum. SD dihitung dengan cara ini (dengan n-1 dalam penyebut) adalah tebakan terbaik Anda untuk nilai SD dalam populasi keseluruhan.

Jika Anda hanya ingin menghitung variasi dalam satu set data tertentu, dan tidak berencana mengekstrapolasi untuk membuat kesimpulan yang lebih luas, maka Anda dapat menghitung SD menggunakan n dalam penyebut. SD yang dihasilkan adalah SD dari nilai-nilai tertentu. Tidak masuk akal untuk menghitung SD dengan cara ini jika Anda ingin memperkirakan SD dari populasi dari mana titik-titik itu diambil. Itu hanya masuk akal untuk menggunakan n dalam penyebut ketika tidak ada pengambilan sampel dari suatu populasi, tidak ada keinginan untuk membuat kesimpulan umum.

Tujuan sains hampir selalu untuk menggeneralisasi, sehingga persamaan dengan n dalam penyebut tidak boleh digunakan. Satu-satunya contoh yang dapat saya pikirkan di mana mungkin masuk akal adalah dalam mengukur variasi antara nilai ujian. Tetapi jauh lebih baik untuk menunjukkan sebaran setiap skor, atau histogram distribusi frekuensi.

Harvey Motulsky
sumber

1

Saya tidak menyarankan itu, saya hanya ingin tahu mengapa perbedaan seperti itu mungkin muncul, tingkat kesalahan seperti apa yang mengikuti saran yang salah mungkin dan apakah ada penjelasan yang layak tentang perbedaan yang dapat saya berikan kepada siswa saya .

Amos

@harvey - tautannya mati

baxx

1

@ baxx .. Terima kasih telah menunjukkan ini. Tetap.

Harvey Motulsky

3

Karena N adalah jumlah poin dalam kumpulan data, orang dapat berargumen bahwa dengan menghitung rata-rata, seseorang telah mengurangi tingkat kebebasan dalam kumpulan data oleh satu (karena seseorang memperkenalkan ketergantungan pada kumpulan data), jadi seseorang harus menggunakan N -1 ketika memperkirakan standar deviasi dari suatu set data yang satu harus memperkirakan rata-rata sebelumnya.

Benjamin Bannier
sumber

Mengapa Sekolah AS dan Inggris mengajarkan berbagai metode Menghitung Deviasi Standar?

Jawaban: