Saat ini saya sedang mempersiapkan wawancara, dan itu mengingatkan saya pada pertanyaan yang pernah saya tanyakan dalam wawancara sebelumnya yang berjalan seperti ini:
"Anda telah diminta untuk merancang beberapa perangkat lunak untuk terus menampilkan 10 istilah penelusuran teratas di Google. Anda diberi akses ke umpan yang menyediakan aliran waktu nyata tanpa akhir dari istilah penelusuran yang saat ini sedang dicari di Google. Jelaskan algoritme dan struktur datanya yang akan Anda gunakan untuk menerapkan ini. Anda harus merancang dua variasi:
(i) Menampilkan 10 istilah pencarian teratas sepanjang masa (yaitu sejak Anda mulai membaca feed).
(ii) Menampilkan hanya 10 istilah penelusuran teratas selama sebulan terakhir, diperbarui setiap jam.
Anda dapat menggunakan perkiraan untuk mendapatkan daftar 10 teratas, tetapi Anda harus membenarkan pilihan Anda. "
Saya gagal dalam wawancara ini dan masih benar-benar tidak tahu bagaimana menerapkannya.
Bagian pertama menanyakan 10 item paling sering dalam sub-urutan yang terus berkembang dari daftar tak terbatas. Saya memeriksa algoritme pemilihan, tetapi tidak dapat menemukan versi online untuk memecahkan masalah ini.
Bagian kedua menggunakan daftar terbatas, tetapi karena banyaknya data yang sedang diproses, Anda tidak dapat benar-benar menyimpan seluruh istilah pencarian dalam memori dan menghitung histogram setiap jam.
Masalahnya menjadi lebih sulit dengan fakta bahwa daftar 10 teratas terus diperbarui, jadi entah bagaimana Anda perlu menghitung 10 teratas Anda melalui jendela geser.
Ada ide?

what is the most frequent item in the subsequence [2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5] of your sequence?Jawaban:
Sepertinya banyak sekali data, dengan biaya yang mungkin mahal untuk menyimpan semua frekuensi. Ketika jumlah data sangat besar sehingga kami tidak dapat menyimpan semuanya, kami memasuki domain algoritme aliran data .
Buku yang berguna di bidang ini: Muthukrishnan - "Aliran Data: Algoritma dan Aplikasi"
Referensi terkait erat dengan masalah yang sedang saya ambil dari yang saya ambil dari atas: Manku, Motwani - "Perkiraan Jumlah Frekuensi atas Aliran Data" [pdf]
Ngomong-ngomong, Motwani, dari Stanford, (sunting) adalah seorang penulis dari buku "Randomized Algorithms" yang sangat penting .
Bab 11 buku ini membahas masalah ini. Sunting: Maaf, referensi buruk, bab itu ada pada masalah yang berbeda. Setelah memeriksa, saya merekomendasikan bagian 5.1.2 dari buku Muthukrishnan , tersedia online.Heh, pertanyaan wawancara yang bagus.
sumber
Ringkasan Estimasi Frekuensi
Ada beberapa algoritme terkenal yang dapat memberikan perkiraan frekuensi untuk aliran semacam itu menggunakan jumlah penyimpanan yang tetap. Salah satunya adalah Frequent, oleh Misra dan Gries (1982). Dari daftar n item, ditemukan semua item yang muncul lebih dari n / k kali, menggunakan k - 1 penghitung. Ini adalah generalisasi dari Boyer dan Moore Mayoritas algoritma (Fischer-Salzberg, 1982), di mana k adalah 2. Manku dan Motwani ini LossyCounting (2002) dan Metwally ini SpaceSaving (2005) dari memiliki persyaratan ruang yang sama, tetapi dapat memberikan perkiraan yang lebih akurat dalam kondisi.
Hal penting yang harus diingat adalah algoritme ini hanya dapat memberikan perkiraan frekuensi. Secara khusus, estimasi Misra-Gries dapat menghitung di bawah frekuensi aktual sebesar (n / k) item.
Misalkan Anda memiliki algoritme yang dapat mengidentifikasi item secara positif hanya jika item tersebut muncul lebih dari 50% sepanjang waktu. Beri makan algoritme ini aliran N item berbeda, lalu tambahkan N - 1 salinan lain dari satu item, x , dengan total 2N - 1 item. Jika algoritme memberi tahu Anda bahwa x melebihi 50% dari total, itu pasti ada di aliran pertama; jika tidak, x tidak ada di aliran awal. Agar algoritme dapat membuat penentuan ini, algoritme harus menyimpan aliran awal (atau ringkasan yang sebanding dengan panjangnya)! Jadi, kita dapat membuktikan pada diri kita sendiri bahwa ruang yang dibutuhkan oleh algoritma yang "tepat" adalah Ω ( N ).
Alih-alih, algoritme frekuensi yang dijelaskan di sini memberikan perkiraan, mengidentifikasi item apa pun yang melebihi ambang batas, bersama dengan beberapa item yang berada di bawahnya dengan margin tertentu. Misalnya algoritma Mayoritas , menggunakan satu penghitung, akan selalu memberikan hasil; jika ada item yang melebihi 50% dari aliran, itu akan ditemukan. Tapi itu mungkin juga memberi Anda item yang hanya muncul sekali. Anda tidak akan tahu tanpa melewati data kedua (sekali lagi, menggunakan satu penghitung, tetapi hanya mencari item itu).
Algoritma yang Sering
Berikut adalah deskripsi sederhana dari algoritma Misra-Gries ' Frequent . Demaine (2002) dan lainnya telah mengoptimalkan algoritme, tetapi ini memberi Anda intinya.
Tentukan fraksi ambang, 1 / k ; item apapun yang muncul lebih dari n / k kali akan ditemukan. Buat peta kosong (seperti pohon merah-hitam); kuncinya adalah istilah penelusuran, dan nilainya akan menjadi penghitung untuk istilah itu.
Perhatikan bahwa Anda dapat memproses data dalam jumlah tak terbatas dengan jumlah penyimpanan tetap (hanya peta berukuran tetap). Jumlah penyimpanan yang dibutuhkan hanya bergantung pada ambang bunga, dan ukuran aliran tidak menjadi masalah.
Menghitung Pencarian
Dalam konteks ini, mungkin Anda menyangga satu jam pencarian, dan melakukan proses ini pada data jam itu. Jika Anda dapat mengambil lintasan kedua di atas log pencarian jam ini, Anda bisa mendapatkan jumlah pasti kemunculan "kandidat" teratas yang diidentifikasi di lintasan pertama. Atau, mungkin tidak apa-apa untuk membuat satu kali lulus, dan melaporkan semua kandidat, mengetahui bahwa item apa pun yang seharusnya ada disertakan, dan tambahan apa pun hanyalah kebisingan yang akan hilang dalam satu jam berikutnya.
Setiap kandidat yang benar-benar melebihi ambang batas minat disimpan sebagai ringkasan. Simpan ringkasan ini selama sebulan, buang yang terlama setiap jamnya, dan Anda akan memiliki perkiraan yang baik untuk istilah penelusuran yang paling umum.
sumber
Ini adalah salah satu proyek penelitian yang sedang saya jalani. Persyaratannya hampir persis seperti milik Anda, dan kami telah mengembangkan algoritme yang bagus untuk menyelesaikan masalah.
Masukan
Masukannya adalah aliran kata atau frasa bahasa Inggris yang tak ada habisnya (kami menyebutnya sebagai
tokens).Hasil
Aplikasi dari penelitian ini adalah untuk menemukan topik hangat atau trend topik di Twitter atau Facebook. Kami memiliki perayap yang merayapi situs web, yang menghasilkan aliran kata-kata, yang akan dimasukkan ke dalam sistem. Sistem kemudian akan mengeluarkan kata atau frase frekuensi teratas baik secara keseluruhan atau secara historis. Bayangkan dalam beberapa minggu terakhir kalimat "Piala Dunia" akan muncul berkali-kali di Twitter. Begitu juga dengan "Paul si gurita". :)
String menjadi Integer
Sistem memiliki ID integer untuk setiap kata. Meskipun ada kemungkinan kata yang hampir tak terbatas di Internet, tetapi setelah mengumpulkan sekumpulan besar kata, kemungkinan menemukan kata-kata baru menjadi semakin rendah. Kami telah menemukan 4 juta kata yang berbeda, dan memberikan ID unik untuk masing-masing kata. Seluruh kumpulan data ini dapat dimuat ke dalam memori sebagai tabel hash, memakan sekitar 300MB memori. (Kami telah mengimplementasikan tabel hash kami sendiri. Implementasi Java membutuhkan overhead memori yang besar)
Setiap frase kemudian dapat diidentifikasi sebagai array bilangan bulat.
Ini penting, karena pengurutan dan perbandingan pada bilangan bulat jauh lebih cepat daripada pada string.
Arsipkan Data
Sistem menyimpan data arsip untuk setiap token. Pada dasarnya itu adalah pasangan
(Token, Frequency). Namun, tabel yang menyimpan data akan sangat besar sehingga kita harus mempartisi tabel secara fisik. Setelah skema partisi didasarkan pada ngram token. Jika token adalah satu kata, itu adalah 1 gram. Jika token adalah frase dua kata, itu adalah 2gram. Dan ini terus berlanjut. Secara kasar pada 4gram kami memiliki 1 miliar rekaman, dengan ukuran tabel sekitar 60GB.Memproses Arus Masuk
Sistem akan menyerap kalimat yang masuk sampai memori digunakan sepenuhnya (Ya, kita membutuhkan MemoryManager). Setelah mengambil N kalimat dan menyimpannya dalam memori, sistem akan berhenti sejenak, dan mulai mengubah setiap kalimat menjadi kata dan frasa. Setiap token (kata atau frase) dihitung.
Untuk token yang sangat sering, mereka selalu disimpan dalam memori. Untuk token yang lebih jarang, mereka diurutkan berdasarkan ID (ingat kita menerjemahkan String ke dalam array bilangan bulat), dan diserialkan ke dalam file disk.
(Namun, untuk masalah Anda, karena Anda hanya menghitung kata, maka Anda dapat meletakkan semua peta frekuensi kata di memori saja. Struktur data yang dirancang dengan cermat hanya akan menggunakan memori 300MB untuk 4 juta kata yang berbeda. Beberapa petunjuk: gunakan karakter ASCII untuk mewakili Strings), dan ini lebih dapat diterima.
Sementara itu, akan ada proses lain yang diaktifkan setelah menemukan file disk yang dihasilkan oleh sistem, lalu mulai menggabungkannya. Karena file disk diurutkan, penggabungan akan mengambil proses yang sama seperti merge sort. Beberapa desain perlu diperhatikan di sini juga, karena kami ingin menghindari pencarian disk yang terlalu banyak secara acak. Idenya adalah untuk menghindari membaca (proses penggabungan) / menulis (keluaran sistem) pada saat yang sama, dan membiarkan proses penggabungan membaca dari satu disk saat menulis ke disk yang berbeda. Ini mirip dengan menerapkan penguncian.
Akhir hari
Pada akhirnya, sistem akan memiliki banyak token yang sering disimpan dalam memori, dan banyak token lain yang lebih jarang disimpan dalam beberapa file disk (dan setiap file diurutkan).
Sistem membersihkan peta dalam memori ke dalam file disk (urutkan). Sekarang, masalahnya adalah menggabungkan satu set file disk yang diurutkan. Dengan menggunakan proses serupa, kami akan mendapatkan satu file disk yang diurutkan di bagian akhir.
Kemudian, tugas akhir adalah menggabungkan file disk yang telah diurutkan ke dalam database arsip. Bergantung pada ukuran database arsip, algoritme bekerja seperti di bawah ini jika cukup besar:
Intuisi adalah bahwa setelah beberapa saat, jumlah penyisipan akan menjadi semakin kecil. Semakin banyak operasi hanya akan memperbarui. Dan pembaruan ini tidak akan dikenakan sanksi oleh indeks.
Semoga penjelasan lengkap ini bisa membantu. :)
sumber
Anda dapat menggunakan tabel hash yang dikombinasikan dengan pohon pencarian biner . Menerapkan
<search term, count>kamus yang memberi tahu Anda berapa kali setiap istilah pencarian telah dicari.Jelas mengulang seluruh tabel hash setiap jam untuk mendapatkan 10 teratas sangat buruk. Tapi ini adalah Google yang sedang kita bicarakan, jadi Anda dapat berasumsi bahwa sepuluh teratas akan mendapatkan, katakanlah lebih dari 10.000 klik (meskipun mungkin jumlahnya jauh lebih besar). Jadi, setiap kali jumlah istilah penelusuran melebihi 10.000, masukkan di BST. Kemudian setiap jam, Anda hanya perlu mendapatkan 10 pertama dari BST, yang seharusnya berisi entri yang relatif sedikit.
Ini memecahkan masalah top-10-of-all-time.
Bagian yang benar-benar sulit adalah menangani satu istilah yang menggantikan posisi lain dalam laporan bulanan (misalnya, "stack overflow" mungkin memiliki 50.000 klik selama dua bulan terakhir, tetapi hanya 10.000 bulan lalu, sementara "amazon" mungkin memiliki 40 000 untuk dua bulan terakhir tetapi 30 000 untuk bulan lalu. Anda ingin "amazon" muncul sebelum "stack overflow" dalam laporan bulanan Anda). Untuk melakukan ini, saya akan menyimpan, untuk semua istilah pencarian utama (di atas 10.000 pencarian sepanjang waktu), daftar 30 hari yang memberi tahu Anda berapa kali istilah tersebut dicari pada setiap hari. Daftar ini akan bekerja seperti antrian FIFO: Anda menghapus hari pertama dan memasukkan yang baru setiap hari (atau setiap jam, tetapi kemudian Anda mungkin perlu menyimpan lebih banyak informasi, yang berarti lebih banyak memori / ruang. Jika memori bukan masalah, lakukan itu, jika tidak gunakan "perkiraan" itu
Ini sepertinya awal yang bagus. Anda kemudian dapat khawatir tentang memangkas istilah yang memiliki> 10.000 klik tetapi belum memiliki banyak dalam waktu yang lama dan hal-hal seperti itu.
sumber
kasus i)
Pertahankan hashtable untuk semua istilah pencarian, serta daftar sepuluh teratas yang diurutkan terpisah dari hashtable. Setiap kali pencarian terjadi, tambahkan item yang sesuai di hashtable dan periksa untuk melihat apakah item itu sekarang harus diganti dengan item ke-10 dalam daftar sepuluh besar.
Pencarian O (1) untuk daftar sepuluh teratas, dan penyisipan max O (log (n)) ke dalam hashtable (dengan asumsi tabrakan dikelola oleh pohon biner penyeimbang diri).
kasus ii) Alih-alih mempertahankan hashtable besar dan daftar kecil, kami mempertahankan daftar hashtable dan diurutkan dari semua item. Setiap kali pencarian dilakukan, istilah itu bertambah dalam hashtable, dan dalam daftar yang diurutkan, istilah tersebut dapat diperiksa untuk melihat apakah itu harus diganti dengan istilah setelahnya. Pohon biner self-balancing dapat bekerja dengan baik untuk ini, karena kita juga harus dapat menanyakannya dengan cepat (lebih lanjut tentang ini nanti).
Selain itu kami juga memelihara daftar 'jam' dalam bentuk daftar FIFO (antrian). Setiap elemen 'jam' akan berisi daftar semua pencarian yang dilakukan dalam jam tertentu. Misalnya, daftar jam buka kami mungkin terlihat seperti ini:
Kemudian, setiap jam: Jika daftar memiliki setidaknya 720 jam (itu adalah jumlah jam dalam 30 hari), lihat elemen pertama dalam daftar, dan untuk setiap istilah penelusuran, kurangi elemen tersebut di hashtable dengan jumlah yang sesuai . Setelah itu, hapus elemen jam pertama dari daftar.
Jadi katakanlah kita berada di jam 721, dan kita siap untuk melihat jam pertama dalam daftar kita (di atas). Kami akan mengurangi item gratis sebesar 56 di hashtable, gambar lucu sebesar 321, dll., Dan kemudian akan menghapus jam 0 dari daftar sepenuhnya karena kami tidak perlu melihatnya lagi.
Alasan kami mempertahankan daftar yang diurutkan dari semua istilah yang memungkinkan kueri cepat adalah karena setiap jam setelah kami menelusuri istilah penelusuran dari 720 jam yang lalu, kami perlu memastikan daftar sepuluh teratas tetap diurutkan. Jadi saat kami mengurangi 'barang gratis' sebanyak 56 di hashtable misalnya, kami akan memeriksa untuk melihat di mana posisinya sekarang dalam daftar. Karena ini adalah pohon biner penyeimbang diri, semua itu dapat diselesaikan dengan baik dalam waktu O (log (n)).
Sunting: Mengorbankan akurasi untuk ruang ...
Mungkin berguna juga untuk menerapkan daftar besar di yang pertama, seperti di yang kedua. Kemudian kita dapat menerapkan pengoptimalan ruang berikut pada kedua kasus: Jalankan tugas cron untuk menghapus semua kecuali item x teratas dalam daftar. Ini akan membuat persyaratan ruang tetap rendah (dan akibatnya membuat kueri di daftar lebih cepat). Tentu saja, ini akan menghasilkan hasil perkiraan, tetapi ini diperbolehkan. x dapat dihitung sebelum menerapkan aplikasi berdasarkan memori yang tersedia, dan disesuaikan secara dinamis jika tersedia lebih banyak memori.
sumber
Berpikir kasar ...
Untuk 10 besar sepanjang masa
Untuk 10 teratas bulanan diperbarui setiap jam:
Errr ... masuk akal? Saya tidak memikirkan ini seperti yang saya lakukan dalam kehidupan nyata
Ah ya, lupa menyebutkan, "penyalinan / perataan" per jam yang diperlukan untuk statistik bulanan sebenarnya dapat menggunakan kembali kode yang sama yang digunakan untuk 10 teratas sepanjang masa, efek samping yang bagus.
sumber
Solusi yang tepat
Pertama, solusi yang menjamin hasil yang benar, tetapi membutuhkan banyak memori (peta besar).
Varian "sepanjang masa"
Pertahankan peta hash dengan kueri sebagai kunci dan dihitung sebagai nilai. Selain itu, simpan daftar 10 kueri yang paling sering sejauh ini dan jumlah hitungan ke-10 yang paling sering (ambang batas).
Perbarui peta secara konstan saat aliran kueri dibaca. Setiap kali hitungan melebihi ambang batas saat ini, lakukan hal berikut: hapus kueri ke-10 dari daftar "10 Teratas", ganti dengan kueri yang baru saja Anda perbarui, dan perbarui juga ambang batas tersebut.
Varian "Bulan lalu"
Pertahankan daftar "Top 10" yang sama dan perbarui dengan cara yang sama seperti di atas. Juga, pertahankan peta yang serupa, tetapi kali ini simpan vektor 30 * 24 = 720 hitungan (satu untuk setiap jam) sebagai nilai. Setiap jam lakukan hal berikut untuk setiap kunci: hapus penghitung terlama dari vektor tambahkan yang baru (diinisialisasi ke 0) di akhir. Hapus kunci dari peta jika vektor semuanya-nol. Selain itu, setiap jam Anda harus menghitung daftar "Top 10" dari awal.
Catatan: Ya, kali ini kami menyimpan 720 bilangan bulat, bukan satu, tetapi ada lebih sedikit kunci (varian sepanjang masa memiliki ekor yang sangat panjang).
Perkiraan
Perkiraan ini tidak menjamin solusi yang benar, tetapi memakan lebih sedikit memori.
sumber
10 istilah penelusuran teratas selama sebulan terakhir
Menggunakan pengindeksan / struktur data yang efisien memori, seperti percobaan yang padat (dari entri wikipedia di mencoba ) kira-kira mendefinisikan beberapa hubungan antara persyaratan memori dan n - jumlah istilah.
Jika memori yang diperlukan tersedia ( asumsi 1 ), Anda dapat menyimpan statistik bulanan yang tepat dan menggabungkannya setiap bulan ke dalam statistik sepanjang waktu.
Ada juga asumsi di sini yang menafsirkan 'bulan lalu' sebagai jendela tetap. Tetapi bahkan jika jendela bulanan bergeser, prosedur di atas menunjukkan prinsip (geser dapat diperkirakan dengan jendela tetap dengan ukuran tertentu).
Ini mengingatkan saya pada database round-robin dengan pengecualian bahwa beberapa statistik dihitung pada 'sepanjang waktu' (dalam arti bahwa tidak semua data dipertahankan; rrd mengkonsolidasikan periode waktu mengabaikan detail dengan rata-rata, menjumlahkan atau memilih nilai max / min, Dalam tugas yang diberikan, detail yang hilang adalah informasi tentang item frekuensi rendah, yang dapat menyebabkan kesalahan).
Asumsi 1
Jika kita tidak dapat menyimpan statistik sempurna selama sebulan penuh, maka kita harus dapat menemukan periode P tertentu yang mana kita harus dapat mempertahankan statistik sempurna. Misalnya, anggap kita memiliki statistik sempurna pada beberapa periode waktu P, yang masuk ke bulan n kali.
Statistik sempurna menentukan fungsi
f(search_term) -> search_term_occurance.Jika kita dapat menyimpan semua
ntabel stat yang sempurna dalam memori maka statistik geser bulanan dapat dihitung seperti ini:ntabel stat yang sempurna)Namun, jika kami hanya mempertahankan 10 teratas pada level agregat (bulanan), maka kami akan dapat membuang banyak data dari statistik lengkap periode tetap. Ini sudah memberikan prosedur kerja yang telah memperbaiki (dengan asumsi batas atas pada tabel stat sempurna untuk periode P) persyaratan memori.
Masalah dengan prosedur di atas adalah jika kita menyimpan info hanya pada 10 istilah teratas untuk jendela geser (serupa untuk semua waktu), maka statistik akan benar untuk istilah pencarian yang memuncak dalam satu periode, tetapi mungkin tidak melihat statistik untuk istilah penelusuran yang terus mengalir dari waktu ke waktu.
Ini dapat diimbangi dengan menyimpan info di lebih dari 10 istilah teratas, misalnya 100 istilah teratas, berharap 10 istilah teratas akan benar.
Saya pikir analisis lebih lanjut dapat menghubungkan jumlah minimum kejadian yang diperlukan agar entri menjadi bagian dari statistik (yang terkait dengan kesalahan maksimum).
(Dalam memutuskan entri mana yang harus menjadi bagian dari statistik, seseorang juga dapat memantau dan melacak tren; misalnya jika ekstrapolasi linier dari kejadian di setiap periode P untuk setiap istilah memberi tahu Anda bahwa istilah tersebut akan menjadi signifikan dalam satu atau dua bulan Anda mungkin sudah mulai melacaknya. Prinsip serupa berlaku untuk menghapus istilah penelusuran dari kumpulan terlacak.)
Kasus terburuk untuk hal di atas adalah ketika Anda memiliki banyak istilah yang hampir sama seringnya dan istilah tersebut berubah sepanjang waktu (misalnya jika melacak hanya 100 istilah, maka jika 150 istilah teratas muncul sama seringnya, tetapi 50 istilah teratas lebih sering di bulan pertama dan jangan sampai beberapa waktu kemudian statistik tidak disimpan dengan benar).
Juga mungkin ada pendekatan lain yang tidak tetap dalam ukuran memori (baik tegasnya juga tidak ada di atas), yang akan mendefinisikan signifikansi minimum dalam hal kejadian / periode (hari, bulan, tahun, sepanjang waktu) untuk menjaga statistik. Ini bisa menjamin kesalahan maksimal di setiap statistik selama agregasi (lihat lagi round robin).
sumber
Bagaimana dengan adaptasi "algoritma penggantian halaman jam" (juga dikenal sebagai "kesempatan kedua")? Saya dapat membayangkannya bekerja dengan sangat baik jika permintaan pencarian didistribusikan secara merata (itu berarti sebagian besar istilah yang dicari muncul secara teratur daripada 5 juta kali berturut-turut dan tidak pernah lagi).
Berikut adalah representasi visual dari algoritma tersebut: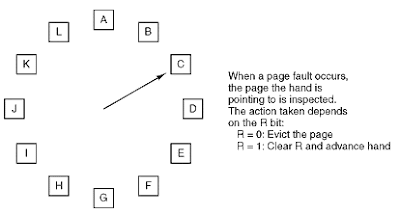
sumber
Simpan jumlah istilah penelusuran dalam tabel hash raksasa, di mana setiap penelusuran baru menyebabkan elemen tertentu bertambah satu. Lacak 20 istilah penelusuran teratas atau lebih; ketika elemen di tempat ke-11 bertambah, periksa apakah perlu menukar posisi dengan # 10 * (tidak perlu menjaga urutan 10 teratas; yang Anda pedulikan hanyalah menggambar perbedaan antara urutan 10 dan 11).
* Pemeriksaan serupa perlu dilakukan untuk melihat apakah istilah penelusuran baru ada di urutan ke-11, jadi algoritme ini juga mengarah ke istilah penelusuran lain - jadi saya menyederhanakan sedikit.
sumber
terkadang jawaban terbaik adalah "Saya tidak tahu".
Aku akan menusuk lebih dalam. Naluri pertama saya adalah memasukkan hasil ke dalam Q. Sebuah proses akan terus memproses item yang masuk ke Q. Proses tersebut akan mempertahankan peta
istilah -> hitung
setiap kali item Q diproses, Anda cukup mencari istilah pencarian dan menambah jumlahnya.
Pada saat yang sama, saya akan menyimpan daftar referensi ke 10 entri teratas di peta.
Untuk entri yang saat ini diterapkan, lihat apakah jumlahnya lebih besar dari jumlah entri terkecil di 10 teratas (jika belum ada dalam daftar). Jika ya, ganti yang terkecil dengan entri.
Saya pikir itu akan berhasil. Tidak ada operasi yang memakan waktu. Anda harus menemukan cara untuk mengatur ukuran peta hitungan. tapi itu seharusnya cukup bagus untuk jawaban wawancara.
Mereka tidak mengharapkan solusi, yang ingin melihat apakah Anda dapat berpikir. Anda tidak perlu menulis solusi saat itu juga ....
sumber
queue,Qadalah huruf :).Salah satu caranya adalah untuk setiap pencarian, Anda menyimpan istilah pencarian tersebut dan cap waktunya. Dengan begitu, menemukan sepuluh teratas untuk periode waktu apa pun hanyalah masalah membandingkan semua istilah penelusuran dalam periode waktu tertentu.
Algoritmanya sederhana, tetapi kekurangannya adalah konsumsi memori dan waktu yang lebih besar.
sumber
Bagaimana dengan menggunakan Splay Tree dengan 10 node? Setiap kali Anda mencoba mengakses nilai (istilah pencarian) yang tidak terdapat di pohon, buang daun apa pun, masukkan nilainya dan akses.
Ide di balik ini sama dengan jawaban saya yang lain . Dengan asumsi bahwa istilah pencarian diakses secara merata / teratur, solusi ini akan bekerja dengan sangat baik.
edit
Seseorang juga dapat menyimpan beberapa istilah pencarian lagi di pohon (hal yang sama berlaku untuk solusi yang saya sarankan di jawaban saya yang lain) agar tidak menghapus node yang mungkin segera diakses lagi. Semakin banyak nilai yang disimpan di dalamnya, semakin baik hasilnya.
sumber
Entah apakah saya memahaminya dengan benar atau tidak. Solusi saya menggunakan heap. Karena 10 item pencarian teratas, saya membangun heap dengan ukuran 10. Kemudian memperbarui heap ini dengan pencarian baru. Jika frekuensi pencarian baru lebih besar dari heap (Max Heap) teratas, perbarui. Abaikan yang frekuensi terkecil.
Tapi, bagaimana menghitung frekuensi pencarian tertentu akan dihitung pada hal lain. Mungkin seperti yang dikatakan semua orang, algoritma aliran data ....
sumber
Gunakan cm-sketch untuk menyimpan hitungan semua pencarian sejak awal, simpan min-heap berukuran 10 dengan itu untuk top 10. Untuk hasil bulanan, simpan 30 cm-sketch / hash-table dan min-heap dengannya, masing-masing dimulai menghitung dan memperbarui dari 30, 29 .., 1 hari terakhir. Sebagai satu hari berlalu, bersihkan yang terakhir dan gunakan sebagai hari 1. Sama untuk hasil per jam, pertahankan 60 tabel hash dan min-heap dan mulai menghitung untuk 60, 59, ... 1 menit terakhir. Setelah satu menit berlalu, bersihkan yang terakhir dan gunakan sebagai menit ke-1.
Hasil bulanan akurat dalam rentang 1 hari, hasil per jam akurat dalam rentang 1 menit
sumber
Masalahnya tidak dapat dipecahkan secara universal ketika Anda memiliki jumlah memori tetap dan aliran token yang 'tak terbatas' (anggap sangat sangat besar).
Penjelasan kasar ...
Untuk melihat alasannya, pertimbangkan aliran token yang memiliki token tertentu (yaitu kata) T setiap token N dalam aliran input.
Juga, asumsikan bahwa memori dapat menyimpan referensi (kata id dan jumlah) hingga paling banyak M token.
Dengan kondisi ini, dimungkinkan untuk membangun aliran input di mana token T tidak akan pernah terdeteksi jika N cukup besar sehingga aliran tersebut berisi token M yang berbeda di antara T.
Ini tidak tergantung pada detail algoritma top-N. Itu hanya tergantung pada batasan M.
Untuk melihat mengapa ini benar, pertimbangkan aliran masuk yang terdiri dari kelompok dua token identik:
di mana a, dan b adalah semua token yang valid tidak sama dengan T.
Perhatikan bahwa dalam aliran ini, T muncul dua kali untuk masing-masing ai dan bi. Namun tampaknya cukup jarang untuk dikeluarkan dari sistem.
Dimulai dengan memori kosong, token pertama (T) akan mengambil slot di memori (dibatasi oleh M). Kemudian a1 akan mengkonsumsi slot, sampai ke a- (M-1) saat M habis.
Ketika aM tiba, algoritma harus menghilangkan satu simbol jadi biarkan itu menjadi T. Simbol berikutnya akan menjadi b-1 yang akan menyebabkan a-1 menjadi flush, dll.
Jadi, T tidak akan menyimpan memori cukup lama untuk membangun hitungan nyata. Singkatnya, algoritme apa pun akan kehilangan token frekuensi lokal yang cukup rendah tetapi frekuensi global yang tinggi (selama streaming).
sumber